あなたにとって最適化って何ですか？

新潟大学教員によるコラム"知見と生活のあいだ"

教員コラム（六花） 2024.10.09

田中環理学部　教授

最適という言葉は誰でも一度は使ったことがあると思います。また、似た用語に最大・最小、最長・最短などがあり、これらは複数のものを比較する際に何かを規準にして使用する言葉です。日常のあらゆる場面において、時間・距離・金額・人数・量・質などを規準にして、選択肢の中からより良いものを選ぼうと意思決定を行う必要があり、そして、最も優れたもの（あるいは好ましいもの）を「最適」と呼び、その求めるプロセス（行為）を「最適化する」と表現します。しかし、「最適化」したつもりが、詳しく検証したり経験値が増すと、もっと好ましいものが見つかったりするものです。

最近、数学が得意な主人公が他分野で活躍するテレビドラマをよく見かけます。これは、多くの人々にとって「数学」の考え方が社会を支えていると認識していることから共感を得て支持されるからだと考えます。実際、数学は古代からたくさん応用されていますが、例を挙げるときりがありません。現代社会に限ってみても、次のようなものがあります。

ラジオ放送やテレビ放送、あるいは携帯電話の通信などに代表される信号処理技術や病院の診療で利用されるコンピュータ断層撮影（CTスキャン）は、ベクトルの内積の原理を利用して組み立てられています。また、コンパクトディスクの読み取り技術やバーコード、QRコード^※などのチェックデジットの仕組みは符号理論に基づいています。さらに、コンピュータネットワークにおいて安心な通信のために、暗号理論を利用した通信技術が必要であることも常識となりました。

一方で、最適化したい問題は意思決定者の考える【対象】と【規準】が多様で、最適化手法も様々です。そのため、どのようにモデル化するかによって、使用される数学も異なり、場合によって全く新しい数学が必要になったりします。例えば、最適化する（優劣を決める）評価規準が関数で表され、対象がある種の数学的構造を持っていれば、うまくモデル化することによりベクトル・行列や微分法を使って求めることができる場合があります。しかし、最適化する評価規準を表す関数がより複雑になると、凸解析学など新しい数学を考える必要が出てきます。また、比較する対象がもっと複雑だったりすると組合せ最適化（メタヒューリスティックス）や集合最適化（変分解析、集合値解析）などの新しい手法が必要となってきます。

どのような食事の組合せが最適なのか？どのような練習方法がチームの戦力を一番向上させるのか？皆さんならどんな最適化問題を思い浮かべますか。

※QRコードは（株）デンソーウェーブの登録商標です。

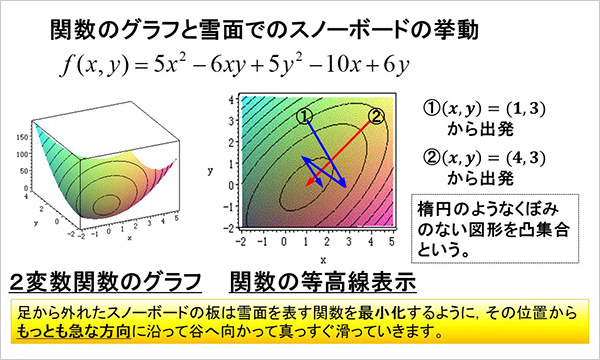非線形計画問題に対する最急降下法の基本原理
（最適性条件や最急降下方向は偏微分の情報を利用）