ロボットモーションプランニングの数学

教員コラム（若手研究者） 2024.11.07

折田龍馬理学部　准教授

ロボットアームは、人間の手と同様の動作（物をつかむ、運ぶ等）を実現する産業用ロボットであり、自動車製造、金属加工など様々な分野で活用されています。
この記事では、図1のようなロボットアームの動作について考えてみましょう。

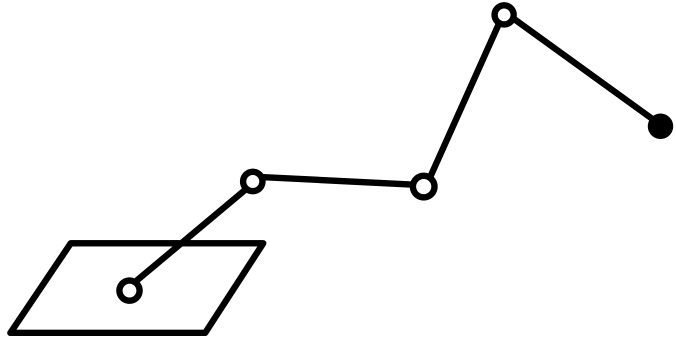
図1　関節（白丸で表記）が4つのロボットアーム

このロボットアームは、関節が自由に動くとします。リモコンで思いのままに動作させても良いですが、ここでは次の問題を考えてみます。

動作のルール（アルゴリズム）をあらかじめ与えることで、任意の状態Aから任意の状態Bへとロボットに自発的に動作させられるか？

この問題をロボットモーションプランニングといいます。ただし、状態A、Bを少しだけ変化させても、動作の過程も少ししか変化しないものを考えます（そうしないと、すべての状態A、Bに対してあらかじめバラバラの動作を決めておけば良いだけになってしまいます）。

この問題をちょっとだけ数学で表してみましょう。まずは簡単に、関節（可動部）が1つだけのロボットアームを考えます。ぐるぐる動かしてみると、先端部分はある球面を描きます。つまり、球面上の各点がロボットアームの1つの状態を表していることになります（図2）。

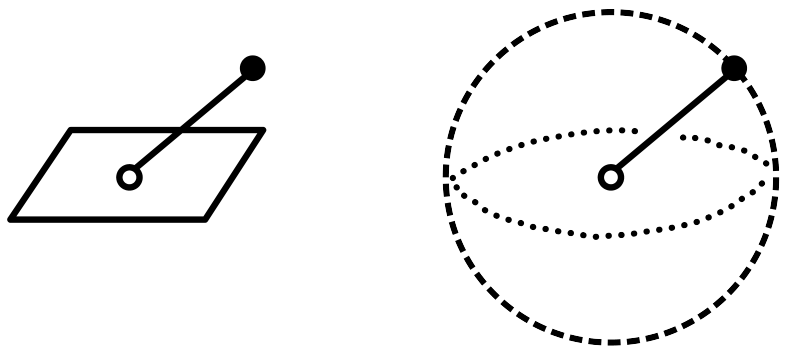
図2　関節が1つのロボットアームの状態は、球面の点と1対1に対応

図1のロボットアームは関節が4つありますから、その状態は4つの球面の点の組で表せます。つまり、状態全体の集合（配位空間といいます）は、球面𝑆²の4つの直積集合𝑆² × 𝑆² × 𝑆² × 𝑆²という8次元の空間になります。すると、状態Aから状態Bへのロボットアームの動作は、𝑆² × 𝑆² × 𝑆² × 𝑆²内の連続曲線であって始点がA、終点がBであるものに対応します。・・・ここから先はより高度な数学の言葉が必要になるのでやめておきます。

結論を述べると、配位空間が可縮であるときに限り、1つのルールでロボットモーションプランニングができることが知られています。可縮とは、連続的に1点に変形できる（潰せる）ことをいいます。球面は中がスカスカの曲面で潰すことができないので、可縮ではありません。つまり、ロボットアームは1つのルールでは自発的に動作させられないことがわかります。

実は、関節が4つのロボットアームを自発的に動作させるには、最低9つのローカルルールが必要であることが知られています。この数を配位空間のtopological complexity（位相的複雑さ）といいます。上の例ではロボットアームの配位空間のtopological complexityを考えましたが、一般の空間（位相空間）に対しても定義することができ、空間の連続変形に関して不変（ホモトピー不変）であることが知られています。一般の空間に対するtopological complexityの決定は全くの未解決で、私も研究テーマの1つにしています。